2024. 1. 29. 07:03ㆍ코딩 도구/LG Aimers
LG Aimers: AI전문가과정 4차
Module 8. 『B2B 고객데이터 기반 예측 단서 스코어링 모델』
ㅇ 교수 : KAIST 박성혁 교수
ㅇ 학습목표
본 모듈은 B2B 고객데이터 기반 예측 단서 스코어링 모델에 대해 학습합니다.
고객의 행동을 예측할 수 있는 방법론과, 추천 시스템에 기반한 고객과 상품을 스코어링하는 방법, 의사결정나무 및 로지스틱 회귀 분석 기반의 고객과 상품을 스코어링하는 방법에 대해 소개합니다.
-로지스틱 회귀분석 vs 선형 회귀분석
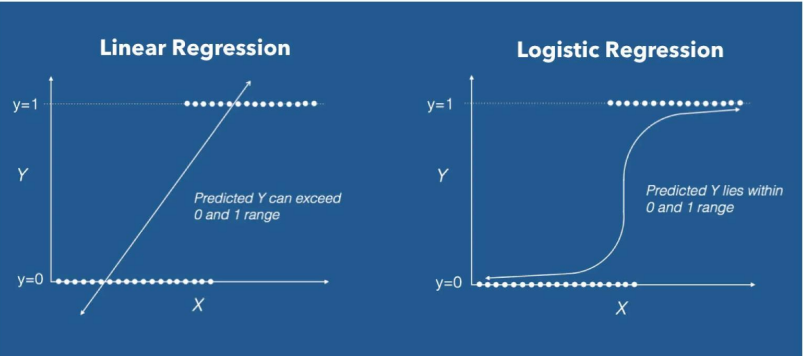
로지스틱 회귀분석은 목적변수가 0 or 1 로 주어지는 binary classification 을 푸는데 최적화되어있음
-로지스틱 회귀분석 어떠할 때 사용되나? 독립변수가 비선형적으로 영향을 미칠 때
[reference] https://modern-manual.tistory.com/entry/%EB%A1%9C%EC%A7%80%EC%8A%A4%ED%8B%B1-%ED%9A%8C%EA%B7%80-%EB%B6%84%EC%84%9D-%EC%98%88%EC%8B%9C%EB%A1%9C-%EC%89%BD%EA%B2%8C-%EC%9D%B4%ED%95%B4%ED%95%98%EA%B8%B0
-로지스틱 회귀분석 주요 수식
O𝑑𝑑𝑠 = 𝑝/1 − 𝑝
오즈는 성공 확률 p(Y=1) 을 실패 확률로 나누어준 값으로, 실패 확률 대비 성공 확률의 비율을 나타낸다.
두 값이 ½ 로 동일하면 Odds = 1 을 갖고, 성공이 0.66, 실패가 0.34 이면 Odds 는 약 2 의 값을 갖는다.
[0, 1] 구간 상에서 움직이는 p 값이 1에 가까워지면 ∞, 0에 가까워지면 0 이 되므로 Odds 값은 [0, ∞] 상에서 분포함
이제 양변에 log 함수를 취하여 값의 분포가 [-∞, ∞] 가 되도록 하면 아래와 같음:
𝑝/1−𝑝 = 𝑒^(α+β𝑋𝑖) , log( 𝑝 / 1−𝑝 ) = α + β𝑋i
결과적으로 보면 Odds 는 선형 모형에 exp 지수함수를 취해준 것에 해당
이제 마지막으로 p(Y=1) 를 기준으로 수식을 재정리하면 [0, 1] 범주를 갖는 Sigmoid 함수로 표현된다:
P(Y=1) = 𝑒^(α+β𝑋𝑖) / (1+𝑒)^(α+β𝑋𝑖 )=1 / (1+𝑒)^−(α+β𝑋𝑖)
최종 수식을 바탕으로 최대우도추정법을 통해 계수(알파와 베타들)를 추정하는 방법론이다.
-Activation Functions

-Logistic Regression vs. ANN
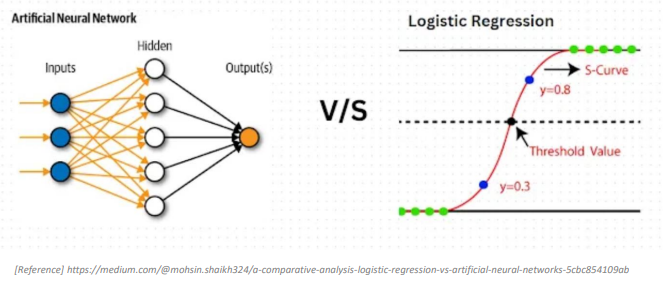
일반적으로 ANN 의 성능이 더 높은 것으로 알려져 있으나, 데이터 볼륨이 적은 상황에서는 로지스틱 회귀분석이 유리할 수 있으며, 결과 해석 측면에서도 (예: 주요 변수 및 가중치) 유리한 부분이 있기 때문에 두 가지 이상의 방법론을 적용하여 B2B 예측분석을 위한 binary classification모형을 개발하고 결과를 비교하는 것을 권장하는 바임
'코딩 도구 > LG Aimers' 카테고리의 다른 글
| LG Aimers 4기 추천 알고리즘 (43) | 2024.01.28 |
|---|---|
| LG Aimers 4기 B2B 고객 행동 예측 방법론 (1) | 2024.01.27 |
| LG Aimers 4기 가치 획득 (0) | 2024.01.26 |
| LG Aimers 4기 고객가치와 가격 (2) | 2024.01.25 |
| LG Aimers 4기 B2B 시장, 소비자와 고객의 차이 (6) | 2024.01.24 |