2024. 2. 11. 13:05ㆍ코딩 도구/기술 & 정보 글 (Tech & Knowledge)
탐색
탐색은 주어진 데이터에서 자신이 원하는 데이터를 찾아내는 알고리즘을 말한다.
주어진 데이터의 성질(정렬 데이터 또는 비정렬 데이터)에 따라 적절한 탐색 알고리즘을 선택하는 것이 중요하고, 실제 모든 코딩 테스트 문제의 기본이 되는 알고리즘이므로 직접 구현해 원리를 완벽하게 이해하는 것이 중요하다.
탐색 영역에서는 그래프를 자주 탐색하므로 아래 저의 블로그를 참고하고 보면 좋을 것 같습니다.
깊이 우선 탐색
깊이 우선 탐색(DFS : depth-first search)은 그래프 완전 탐색 기법 중 하나입니다. 깊이 우선 탐색은 그래프의 시작 노드에서 출발하여 탐색할 한 쪽 분기를 정하여 최대 깊이까지 탐색을 마친 후 다른 쪽 분기로 이동하여 다시 탐색을 수행하는 알고리즘이다.
다음은 깊이 우선 탐색의 기능, 특징, 시간 복잡도를 표로 정리한 것이다. 표의 시간 복잡도는 노드 개수를 V, 에지 개수를 E로 표시했다.
| 기능 | 특징 | 시간 복잡도(노드 수: V, 에지 수: E) |
| 그래프 완전 탐색 | 1. 재귀 함수로 구현 2. 스택 자료구조 이용 |
O(V+E) |
깊이 우선 탐색은 실제 구현 시 재귀 함수를 이용하므로 스택 오버플로 Stack overflow에 유의해야 합니다. 깊이 우선 탐색을 응용하여 풀 수 있는 문제는 단절점 찾기, 단절선 찾기, 사이클 찾기, 위상 정렬 등이 있다.
깊이 우선 탐색의 핵심 이론
DFS는 한 번 방문한 노드를 다시 방문하면 안 되므로 노드 방문 여부를 체크할 리스트가 필요하며, 그래프는 인접 리스트로 표현하고 DFS의 탐색 방식은 후입선출 특성을 가지므로 스택을 사용하여 설명합니다.
여기서는 설명의 편의를 위해 스택을 사용하겠지만 DFS 구현은 스택보다는 스택 성질을 갖는 재귀 함수로 많이 구현한다.
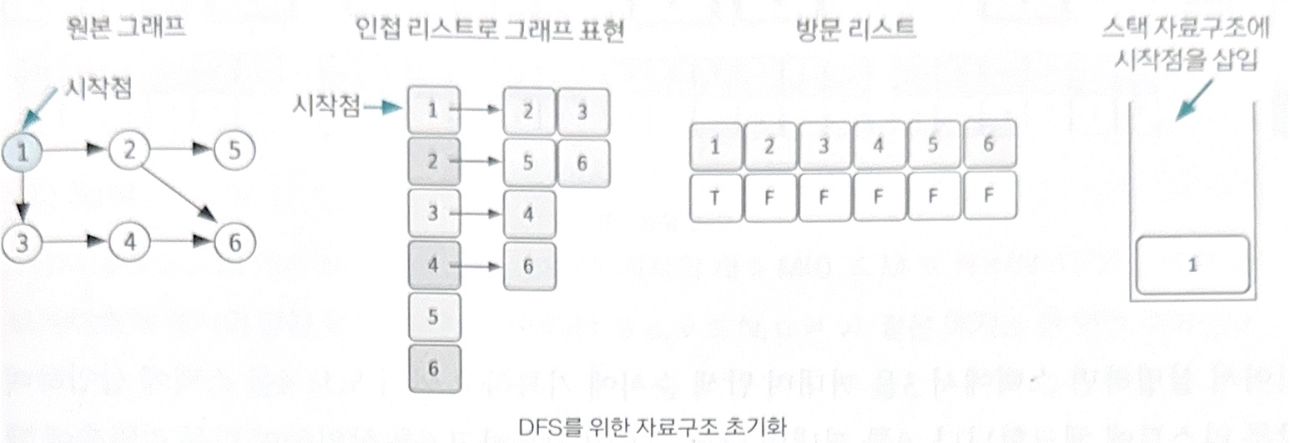
1. DFS를 시작할 노드를 정한 후 사용할 자료구조 초기화하기
DFS를 위해 필요한 초기 작업은 인접 리스트로 그래프 표현하기, 방문 리스트 초기화하기, 시작 노드 스택에 삽입하기다. 스택에 시작 노드를 1로 삽입할 때 해당 위치의 방문 리스트를 체크하면 T, F, F, F, F, F가 된다.
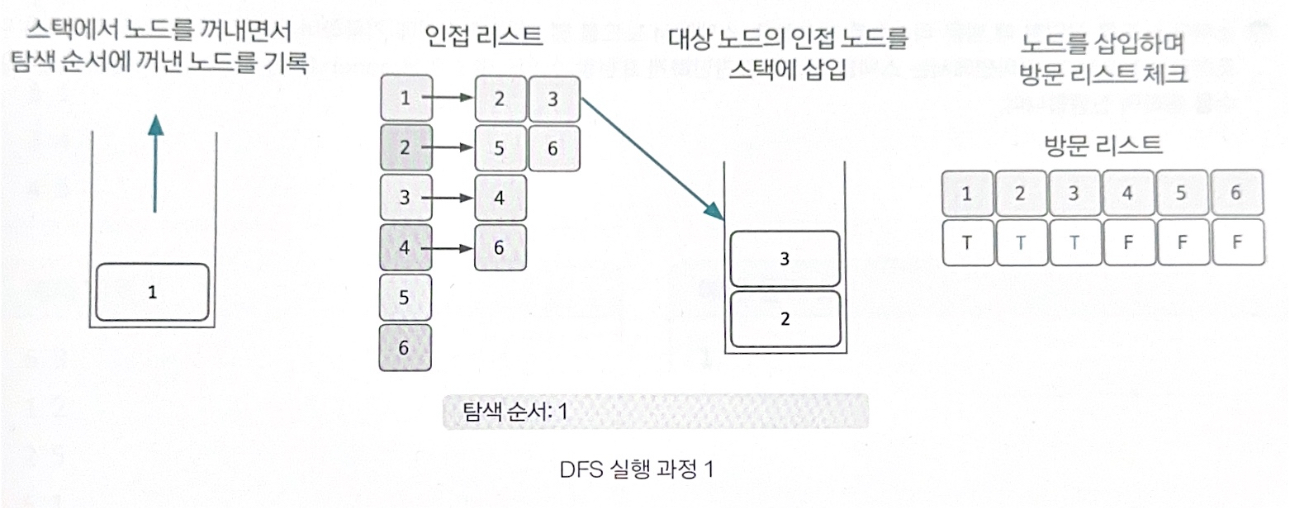
2. 스택에서 노드를 꺼낸 후 꺼낸 노드의 인접 노드를 다시 스택에 삽입하기
이제 pop을 수행하여 노드를 꺼낸다. 꺼낸 노드를 탐색 순서에 기입하고 인접 리스트의 인접 노드를 스택에 삽입하며 방문 리스트를 체크한다. 방문 리스트는 T, T, T, F, F, F가 된다.
3. 스택 자료구조에 값이 없을 때까지 반복하기
앞선 과정을 스택 자료구조에 값이 없을 때까지 반복한다. 이때 이미 다녀간 노드는 방문 리스트를 바탕으로 재삽입하지 않는 것이 핵심이다.
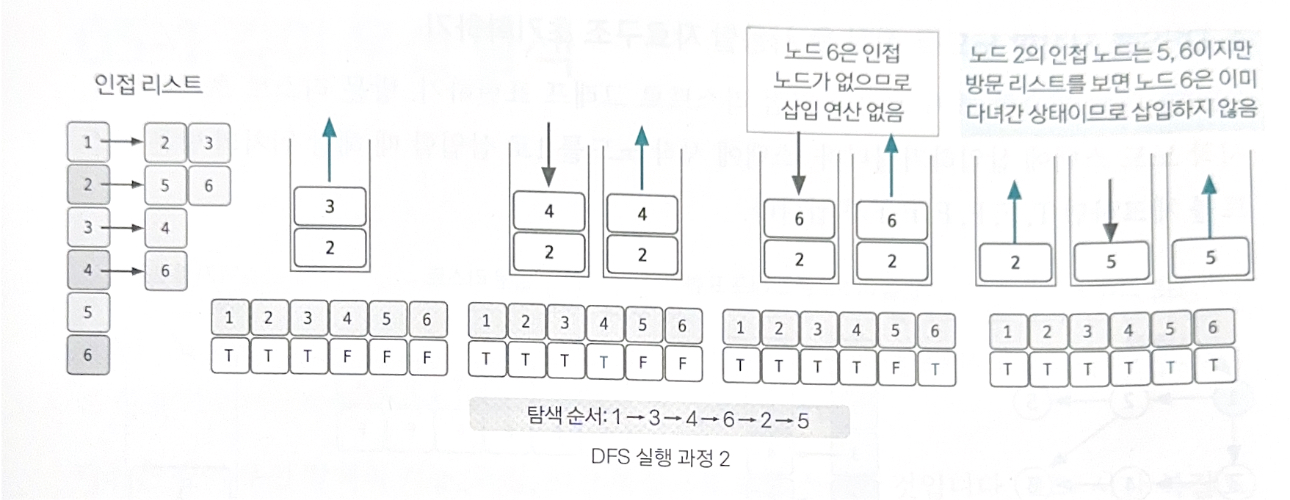
이어서 설명하면 스택에서 3을 꺼내며 탐색 순서에 기록하고 인접 노드 4를 스택에 삽입하며 방문 리스트에 체크한다. 4를 꺼내며 탐색 순서에 기록하고 6을 삽입하며 방문 리스트에 체크한다. 6을 꺼내며 탐색 순서에 기록하고 6과 인접한 노드는 없으므로 추가 삽입은 없다. 계속해서 스택에서 2를 꺼내며 탐색 순서에 기록하고 2와 인접한 5, 6을 삽입하기 위해 본다. 이때 6은 방문 리스트에 T로 체크되어 있으므로 5만 삽입한다. 이 과정을 스택이 빌 때까지 진행한다.
스택에 노드를 삽입할 때 방문 리스트를 체크하고, 스택에서 노드를 뺄 때 탐색 순서에 기록하며 인접 노드를 방문 리스트와 대조하여 살펴본다. 파이썬에서는 스택을 리스트로 간단하게 표현할 수 있으며 삽입은 append() 함수, 꺼내는 작업은 pop() 함수를 통하여 진행한다.
너비 우선 탐색
너비 우선 탐색(BFS, breath-first search)도 그래프를 완전 탐색하는 방법 중 하나로, 시작 노드에서 출발해 시작 노드를 기준으로 가까운 노드를 먼저 방문하면서 탐색하는 알고리즘이다.
| 기능 | 특징 | 시간 복잡도(노드 수: V, 에지 수: E) |
| 그래프 완전 탐색 | 1. FIFO 탐색 2. Queue 자료구조 이용 |
O(V+E) |
너비 우선 탐색은 선입선출 방식으로 탐색하므로 큐를 이용해 구현한다. 또한 너비 우선 탐색은 탐색 시작 노드와 가까운 노드를 우선하여 탐색하므로 목표 노드에 도착하는 경로가 여러 개일 때 최단 경로를 보장한다.
너비 우선 탐색의 핵심 이론
BFS의 원리를 3단계로!
1. BFS를 시작할 노드를 정한 후 사용할 자료구조 초기화하기
BFS도 DFS와 마찬가지로 방문했던 노드는 다시 방문하지 않으므로 방문한 노드를 체크하기 위한 리스트가 필요하다. 그래프를 인접 리스트로 표현하는 것 역시 DFS와 동일하다. 하나 차이점이 있다면 탐색을 위해 스택이 아닌 큐를 사용한다.
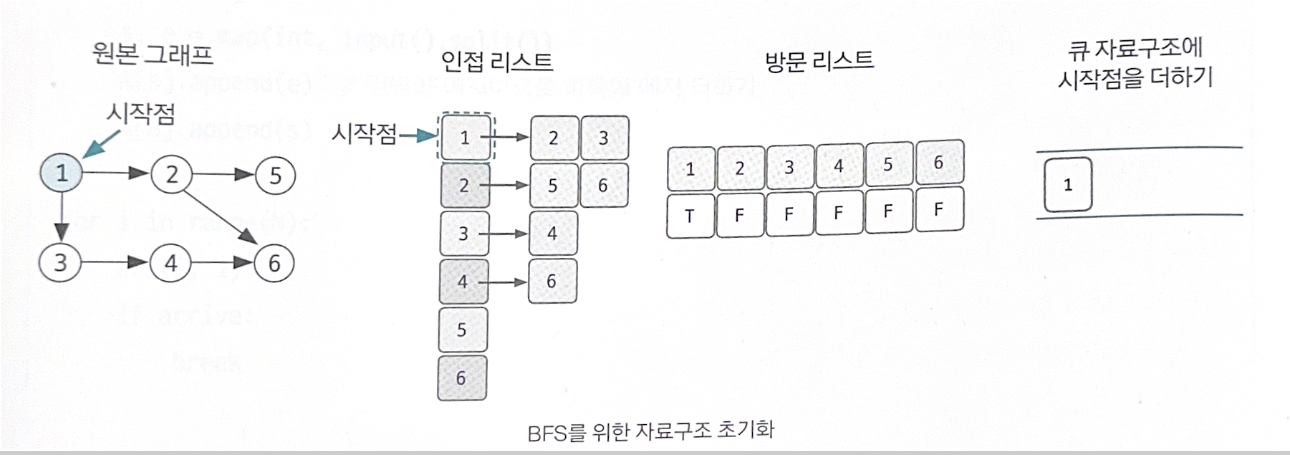
위 그림은 시작 노드를 큐에 삽입하며 방문 리스트를 체크한 것을 보여 준다.
2. 큐에서 노드를 꺼낸 후 꺼낸 노드의 인접 노드를 다시 큐에 삽입하기
큐에서 노드를 꺼내면서 인접 노드를 큐에 삽입한다. 이때 방문 리스트를 체크하여 이미 방문한 노드는 큐에 삽입하지 않는다. 또한 큐에서 꺼낸 노드는 탐색 순서에 기록한다.
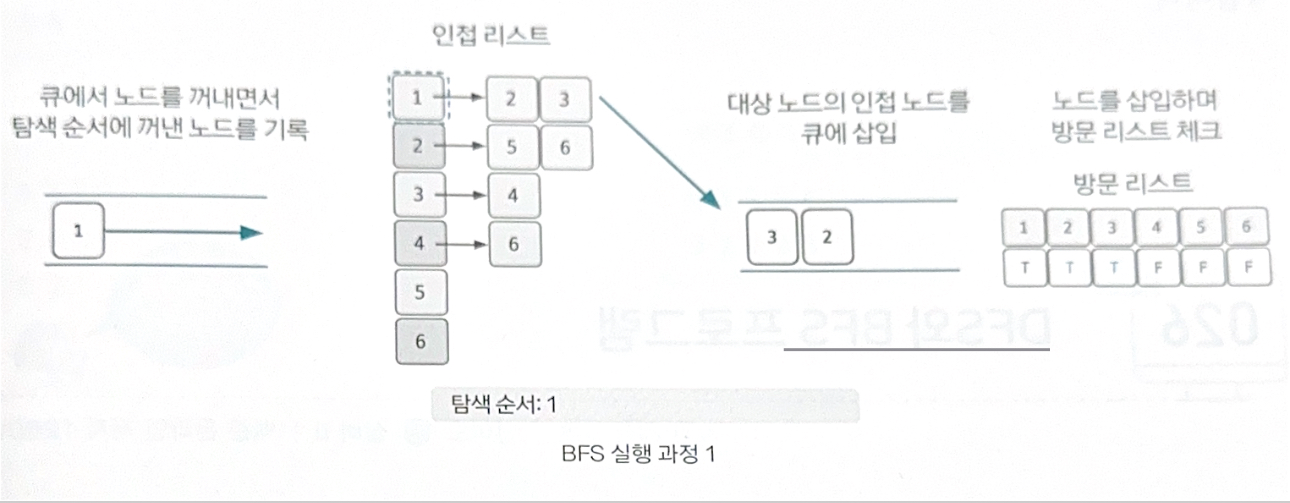
위 그림의 경우 1을 꺼내며 탐색 순서에 1을 기록하고 인접 노드 3, 2를 큐에 삽입하며 방문 리스트에 체크했다.
3. 큐 자료구조에 값이 없을 때까지 반복하기
큐에 노드가 없을 때까지 앞선 과정을 반복한다. 선입선출 방식으로 탐색하므로 탐색 순서 가 DFS와 다름을 확인해 보자.
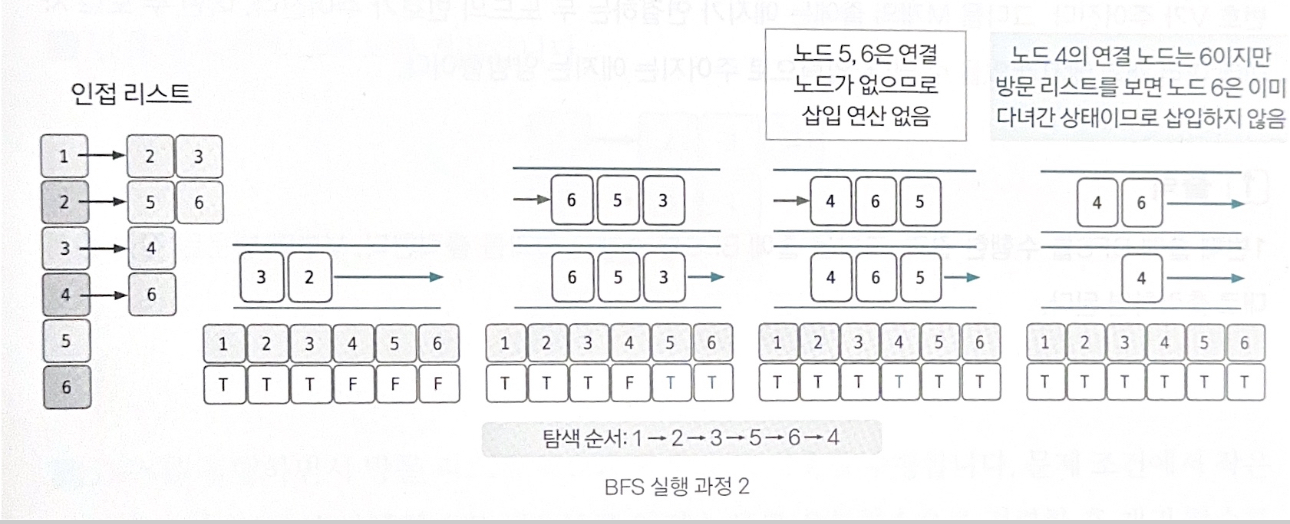
2, 3 순서로 노드를 꺼내며 인접 노드를 큐에 삽입한다. 2의 경우 5, 6은 아직 방문한 적이 없으므로 방문 리스트를 체크하며 모두 삽입한다. 3의 경우 4 역시 방문한 적이 없으므로 방문 리스트를 체크하며 삽입한다. 탐색 순서는 2, 3이 기록됩니다. 5, 6을 꺼낼 때는 인접 노드가 없으니 탐색 순서에 기록만 하고 꺼낸다. 4를 꺼낼 때는 인접 노드가 6이지만 이미 앞서 방문했으므로 6은 큐에 삽입하지 않고 꺼내기만 한다. 최종 탐색 순서는 1, 2, 3, 5, 6, 4 다.
이진 탐색
이진 탐색(binary search)은 데이터가 정렬돼 있는 상태에서 원하는 값을 찾아내는 알고리즘이다. 대상 데이터의 중앙값과 찾고자 하는 값을 비교해 데이터의 크기를 절반씩 줄이면서 대상을 찾는다.
| 기능 | 특징 | 시간 복잡도 |
| 타깃 데이터 탐색 | 중앙값 비교를 통한 대상 축소 방식 | O(logN) |
이진 탐색은 정렬 데이터에서 원하는 데이터를 탐색할 때 사용하는 가장 일반적인 알고리즘 이다. 구현 및 원리가 비교적 간단하므로 많은 코딩 테스트에서 부분 문제로 요구하는 영역이다.
이진 탐색의 핵심 이론
이진 탐색은 오름차순으로 정렬된 데이터에서 다음 4가지 과정을 반복한다.
• 내림차순이라면 조건을 반대로 하여 과정을 반복하면 된다.
이진 탐색 과정
1. 현재 데이터셋의 중앙값을 선택한다.
2. 중앙값 > 타깃 데이터일 때
중앙값 기준으로 왼쪽 데이터셋을 선택한다.
3. 중앙값 < 타깃 데이터일 때
중앙값 기준으로 오른쪽 데이터셋을 선택한다.
4. 과정 1~3을 반복하다가 중앙값 == 타깃 데이터일 때 탐색을 종료한다.
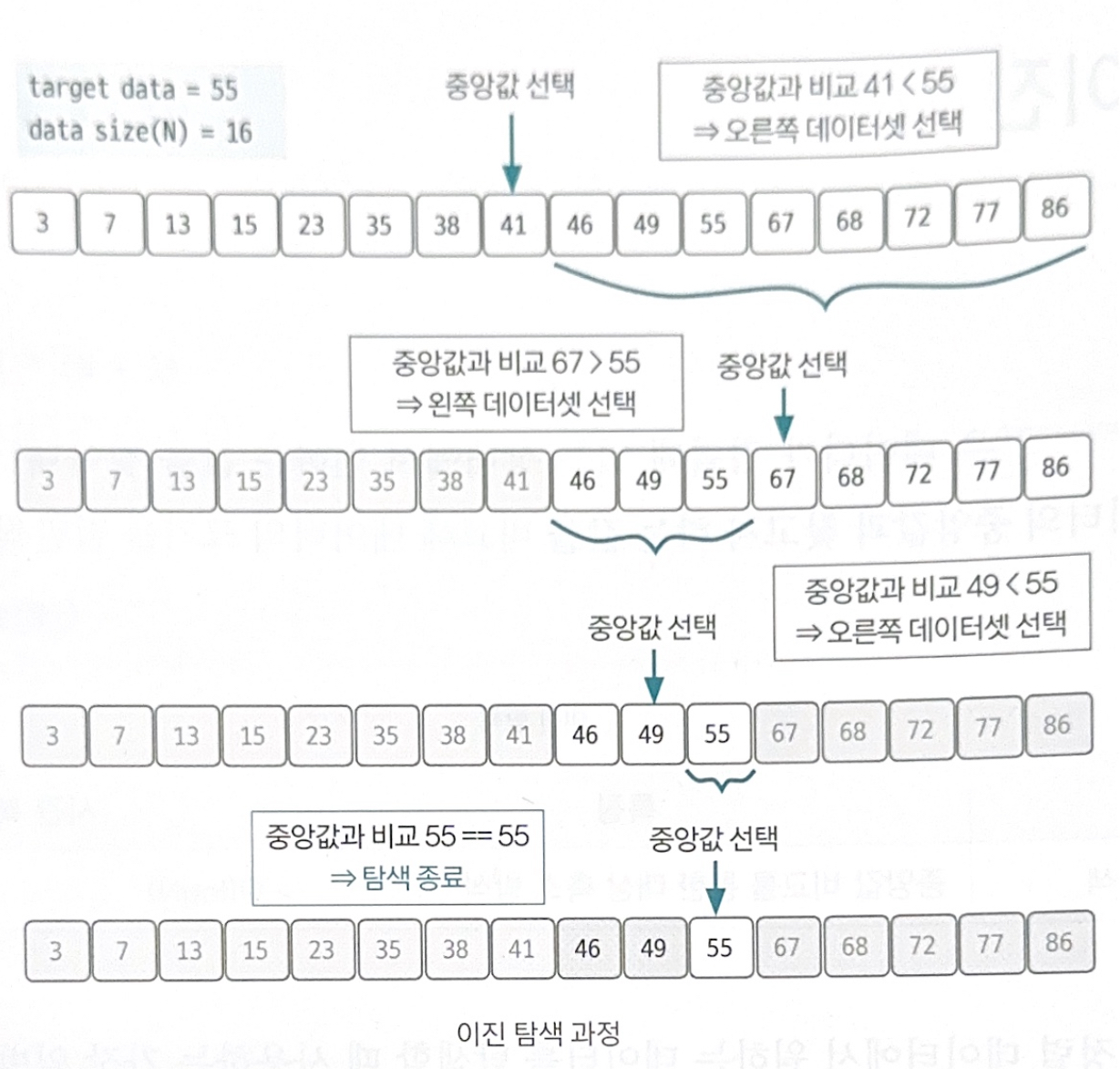
이렇게 이진 탐색을 사용하면 N개의 데이터에서 logN번의 연산으로 원하는 데이터의 위치 찾을 수 있다.
예를 들어 16개의 데이터면 최대 4번의 연산으로 원하는 데이터의 위치 찾을 수 있다. 다만 이진 탐색은 데이터가 정렬되어 있어야 한다. 이런 특징을 잘 염두에 두고 문제를 풀어야 한다.
책 <Do It! 알고리즘 코딩테스트>_김종관 지음, 이지스퍼블리싱 출판사
학교 알고리즘 수업 강의자료 등 여러 자료 참고해서 공부함.
'코딩 도구 > 기술 & 정보 글 (Tech & Knowledge)' 카테고리의 다른 글
| 정수론 : 소수 구하기 에라토스테네스의 채 (38) | 2024.02.16 |
|---|---|
| 그리디 알고리즘과 우선순위 큐 (37) | 2024.02.15 |
| 그래프의 표현 (알고리즘, 자료구조) (32) | 2024.02.10 |
| 정렬 알고리즘 (버블 정렬, 선택 정렬, 삽입 정렬, 퀵 정렬, 병합 정렬, 기수 정렬) (47) | 2024.02.07 |
| 컴퓨터 네트워크의 기본 개념과 동작 원리 (48) | 2024.01.30 |