백준 17298 파이썬 , 스택의 후입선출 성질 이용
2024. 2. 13. 17:08ㆍ코딩 도구/백준
반응형
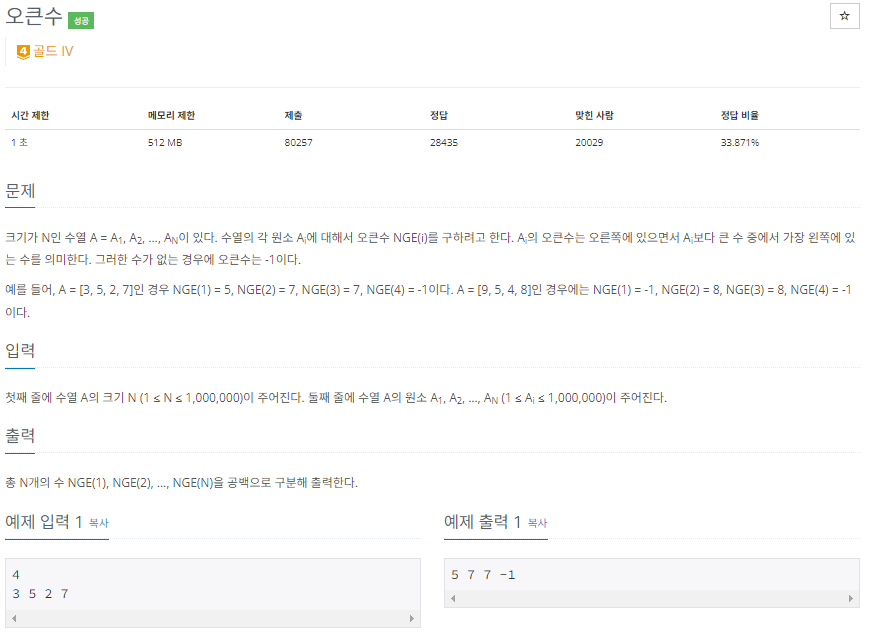
백준 17298 : 오큰수
문제
https://www.acmicpc.net/problem/17298
17298번: 오큰수
첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000,000)이 주어진다. 둘째 줄에 수열 A의 원소 A1, A2, ..., AN (1 ≤ Ai ≤ 1,000,000)이 주어진다.
www.acmicpc.net
답안 코드 :
import sys
n = int(sys.stdin.readline())
A = list(map(int, sys.stdin.readline().split()))
ans = [-1] * n
myStack = []
for i in range(n):
while myStack and A[myStack[-1]] < A[i]:
ans[myStack.pop()] = A[i]
myStack.append(i)
print(" ".join(map(str, ans)))
생각 :
# 문제 분석
# N의 최대 크기 (1 ≤ N ≤ 1,000,000)
# 따라서 반복문을 사용하면 시간초과 날 듯.
# 아이디어
# 스택에 새로 들어오는 수가 top에 존재하는 수보다 크면 그 수는 오큰수
# 오큰수를 구한 후 수열에서 오큰수가 존재하지 않으면 -1 출력
# 문제 푸는 순서
# 1. 스택이 재워져 있고 A[index]> A[top]인 경우 pop한 인덱스를 이용하여 정답 수열에 오큰수를 저장.
# pop은 조건을 만족하는 동안 계속 반복.
# 2. 현재 인덱스를 스택에 push(append)하고 다음 인덱스로 넘어갑니다.
# 3. 과정 1~2를 수열 길이만큼 반복한 다음 현재 스택에 남아 있는 인덱스에 -1을 저장합니다.
# 슈도 코드
# while 스택이 비지 않고, 현재 수열값이 top에 해당하는 수열보다 클 때까지:
# 스택에서 pop한 값을 index로 하는 정답 리스트 부분을 수열 리스트의 현재 값(A[i])으로 저장 스택에 i의 값을 저장
# import sys
# input =sys.stdin.readline()
n = int(input())
ans = [0] * n
A = list(map(int, input().split()))
myStack = []
for i in range(n):
# 스택이 비어 있지 않고 현재 수열이 스택 top 인덱스가 가리키는 수열보다 클 경우
while myStack and A[myStack[-1]] < A[i]:
ans[myStack.pop()] = A[i] # 정답 배열에 오큰수를 현재 수열로 저장하기
myStack.append(i)
while myStack: # 반복문을 다 돌고 나왔는데 스택이 비어 있지 않다면 빌 때까지
ans[myStack.pop()] = -1 #스 택에 쌓인 index에 -1을 넣기
result =""
for i in range(n):
result += str(ans[i])+" "
print(result)
#### 위의 코드가 시간초과
import sys
n = int(sys.stdin.readline())
A = list(map(int, sys.stdin.readline().split()))
ans = [-1] * n
myStack = []
for i in range(n):
while myStack and A[myStack[-1]] < A[i]:
ans[myStack.pop()] = A[i]
myStack.append(i)
print(" ".join(map(str, ans)))
# 시간 복잡도를 줄이기 위해서
# 정답 배열 초기화: 초기에 모든 값이 -1로 초기화되어 있기 때문에 따로 초기화를 할 필요가 없다.
# 결과 출력: 마지막에 리스트를 문자열로 변환하여 출력하는 부분을 한 줄로 처리.
# 스택의 후입선출이라는 성질을 이용하면 종종 시간 복잡도를 줄이거나 특정 문제를 해결하는 도구가 되는 것 같다.
반응형
'코딩 도구 > 백준' 카테고리의 다른 글
| 백준 11286 파이썬 우선순위 큐 sys.stdout.write (37) | 2024.02.16 |
|---|---|
| 백준 2164 파이썬 큐 이해 문제 Queue (29) | 2024.02.15 |
| 백준 1847 파이썬 , 스택의 원리 이용 (35) | 2024.02.11 |
| 백준 11003 파이썬, 덱 구현해서 정렬(슬라이딩 윈도우) (42) | 2024.02.09 |
| 백준 12891 파이썬 , 슬라이딩 윈도우 알고리즘 (41) | 2024.02.08 |