2024. 5. 31. 06:26ㆍ코딩 도구/백준
백준 11689 - GCD(n, k) = 1
문제
https://www.acmicpc.net/problem/11689
11689번: GCD(n, k) = 1
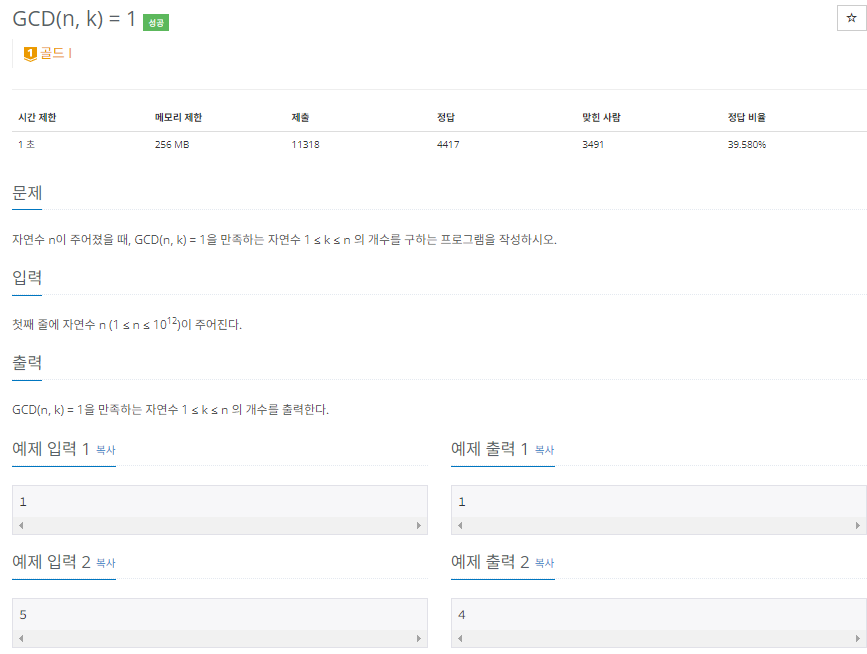
자연수 n이 주어졌을 때, GCD(n, k) = 1을 만족하는 자연수 1 ≤ k ≤ n 의 개수를 구하는 프로그램을 작성하시오.
www.acmicpc.net
답안 코드 :
생각 :
정수론 정리 글들
정수론 : 소수 구하기 에라토스테네스의 채
소수 소수 구하기의 핵심 이론 소수를 구하는 대표적인 판별법으로는 에라토스테네스의 체를 들 수 있다. 에라토스테네스의 체 원리는 다음과 같다. ① 구하고자 하는 소수의 범위만큼 1차원 리
mkisos.tistory.com
https://mkisos.tistory.com/entry/%EC%A0%95%EC%88%98%EB%A1%A0-%EC%98%A4%EC%9D%BC%EB%9F%AC-%ED%94%BC
정수론 : 오일러 피
오일러 피 오일러 피 함수 P[N]의 정의는 1부터 N까지 범위에서 N과 서로소인 자연수의 개수를 뜻한다. 오일러 피 함수는 증명 과정을 공부해야 완벽하게 알 수 있다고하지만 실제 코딩 테스트에
mkisos.tistory.com
정수론 : 유클리드 호제법
유클리드 호제법 유클리드 호제법 euclidean-algorithm은 두 수의 최대 공약수를 구하는 알고리즘이다. 일반적으로 최대 공약수를 구하는 방법은 소인수 분해를 이용한 공통된 소수들의 곱으로 표현
mkisos.tistory.com
정수론 : 확장 유클리드 호제법
확장 유클리드 호제법 유클리드 호제법의 목적이 두 수의 최대 공약수를 구하는 것이라면 확장 유클리드 호제법의 목적은 방정식의 해를 구하는 것이다. 확장 유클리드 호제법을 제대로 이해하
mkisos.tistory.com
'코딩 도구 > 백준' 카테고리의 다른 글
| 백준 1850 파이썬 최대 공약수를 유클리드 호제법 (17) | 2024.06.02 |
|---|---|
| 백준 1934 파이썬 유클리드 호제법 (20) | 2024.06.01 |
| 백준 1016 파이썬 에라토스테네스의 체 방식으로 제곱수의 배수 형태로 탐색 (25) | 2024.05.30 |
| 백준 1747 파이썬 에라토스테네스의 체를 이용 팰린드롬 (20) | 2024.05.29 |
| 백준 1456 파이썬 거의 소수 (1) | 2024.05.28 |